Flächenberechnung
Unter Planimetrie versteht man allgemein metrische Problemstellungen der ebenen Geometrie, insbesondere die Flächeninhaltsberechnung in der Ebene. Der Flächeninhalt einfacher Flächen in der Ebene kann aus bekannten Längenwerten berechnet werden. Die Errechnung komplizierterer Flächen wird meist über Zerlegung in Flächenstücke, die sich leichter errechnen lassen, erreicht.
Quadrat
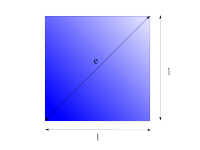
|
|
Rechteck
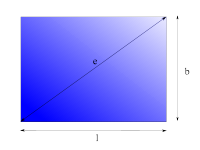
|
|
Parallelogramm
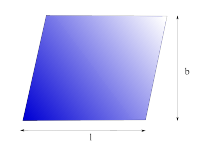
|
Trapez
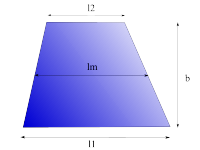
|
Dreieck
Ungleichseitiges Dreieck

|
|
Gleichseitiges Dreieck
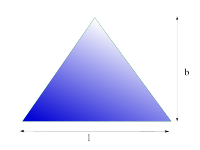
|
|
Regelmäßiges Sechseck
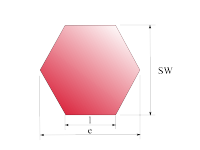
|
|
Kreis
Vollkreis
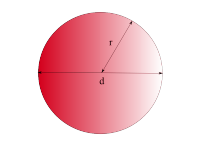
|
|
Kreisausschnitt (Sektor)
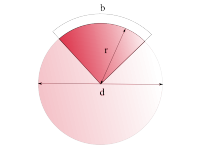
|
Fehler beim Parsen (Syntaxfehler): {\displaystyle A=\frac{d^2 \cdot \pi}{4 \cdot 360°} \cdot \alpha}
|
Kreisabschnitt (Segment)
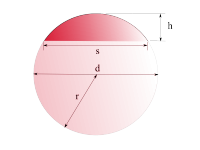
|
|
Kreisring
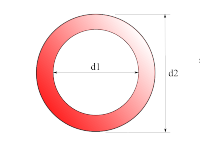
|
|
Elipse
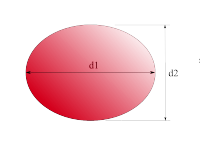
|