Quadratische Funktionen

Unter einer quadratischen Funktion versteht man ein Funktion, die in der Form siehe Definition, vorliegt. Es handelt sich hierbei um ein Polynom zweiten Grades.

Definition

Normalform

$f(x)=a{x}^2+bx+c$ mit $a\ne 0$

Scheitelform (auch Scheitelpunktform)

$y={(x+a)}^2+b$

Funktionsgrafen von quadratischen Funktionen

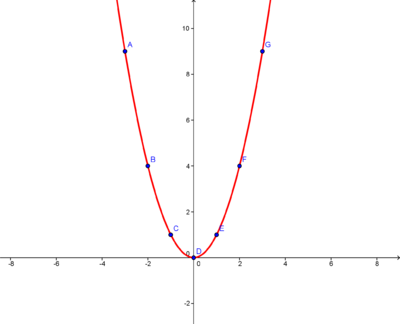
Eine Normalparadbel mit der Funktion $y=x^2$ kann in ein Koordinatensystem eingezeichnet werden, indem eine Wertetabelle nach folgendem Beispiel erstellt wird.

x y A -3 9 B -2 4 C -1 1 D 0 0 E 1 1 F 2 4 G 3 9

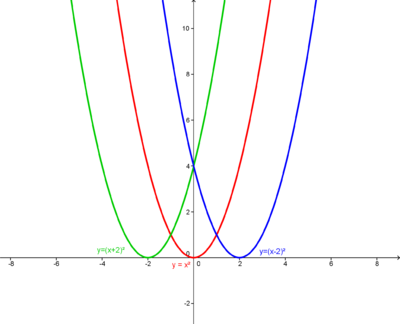
Verschiebung von Funktionsgrafen auf der x-Achse

Verschiebt man die Normalparabel $y=x^2$ um $-a$ auf der x-Achse, so erhält man $y={(x+a)}^2$. Der Funktionsgraf von $y={(x+a)}^2$ ist also eine Normalparabel mit dem Scheitelpunkt $(-a;0)$. Es hängt nur vom Vorzeichen ab, ob die Parabel nach links, oder nach rechts verschoben wird.

• Ist $a$ positiv, so ist $-a$ negativ oder
• ist $a$ negativ, so ist $-a$ positiv.

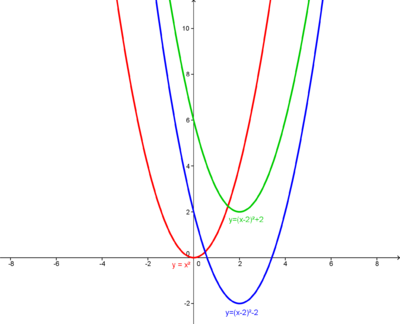
Verschiebung von Funktionsgrafen auf der x- und y-Achse

Liegt eine quadratische Funktion in der Form $y={(x+a)}^2+b$ vor, verschiebt man die Normalparabel um $-a$ entlang der x-Achse und dann um $b$ entlang der y-Achse. Der Scheitelpunkt ist somit durch $(-a;b)$ definiert.

Liegt die Funktion in der Form $y=x^2+px+q$ vor, kann $a$ und $b$ wie folgt ermittelt werden.

$a=\frac{p}{2};$

$b=q-\frac{p^2}{4}$

Siehe auch

• Funktionen
• Gleichungen
• Lineare Funktion
• Formelsammlung Mathematik
• Formelsammlung Höhere Mathematik

Weblinks

• arndt-bruenner.de Der Scheitelpunkt quadratischer Funktionen.