Analog-Digital-Umsetzer
Ein Analog-Digital-Umsetzer ADU (auch Analog-Digital-Wandler oder A/D-Wandler) setzt nach unterschiedlichen Methoden analoge Eingangssignale in digitale Daten bzw. einen Datenstrom um, die dann weiterverarbeitet oder gespeichert werden können.
Kennwerte
Quantisierungseinheit
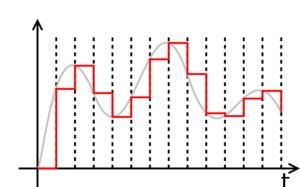
Durch die Abtastung und die nachfolgende Quantisierung (Darstellung einer Größe in einem System, in dem sie nur diskrete Werte annehmen kann) des analogen Signals entstehen Informationsverluste, welche sich bei einer erhöhung der Abtastrate verkleinern. Um das Signal später richtig rekonstruieren zu können (Alias-Effekt), muss die Abtastfrequenz aber mindestens das Doppelte der maximal möglichen Eingangsfrequenz betragen (Nyquist-Frequenz).
Die binare Zahl am Ausgang des AD-Umsetzers gibt an, wie oft eine elementare Quntisierungseinheit in der analogen Eingangsgröße vorhanden ist.
Quantisierungsstufen
Die Anzahl der Quantisierungsstufen Zmax lässt sich in Bit (N) angeben und mit folgender Formel berechnen.
Quantisierungsfehler
Der Quantisierungsfehler lässt sich wie folgt berechnen.
Realisierung
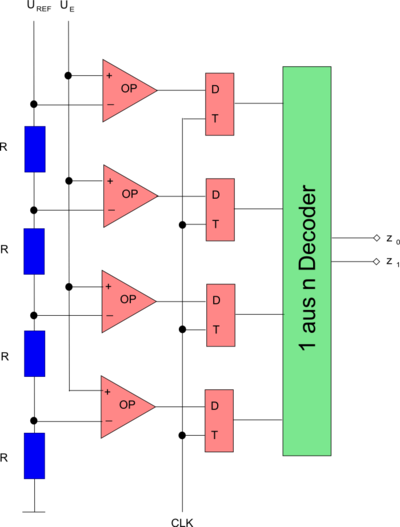
Parallelverfahren
Dieses Verfahren ist kompliziert und aufwendig umzusetzen, dafür aber sehr schnell. Mit Spannungsteilern werden alle möglichen Ausgangsspannungen erzeugt, und mit Hilfe eines 1 aus n-Decoder wird die gewünschte Spannung ausgewählt. Das Parallelverfahren erfordert ZMAX Schalter!
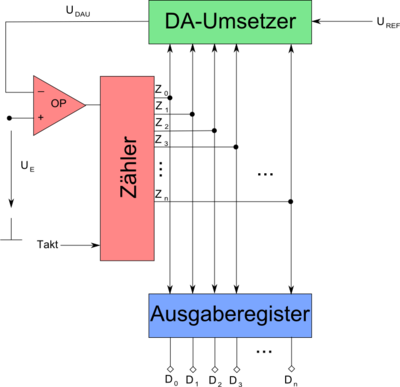
Zählverfahren
Das Zählverfahren gewinnt zunehmend an Bedeutung, da der Pulsbreitenmodulator eine einfach zu integrierende Schaltung ist.
Einflanken-AD-Umsetzer (Single-Slope)
Dieses Verfahren ist nur von geringer Bedeutung da ungenau. Besser ist die Weiterentwicklund das Dual-Slope-Verfahren (Zweiflanken-AD-Umsetzer).
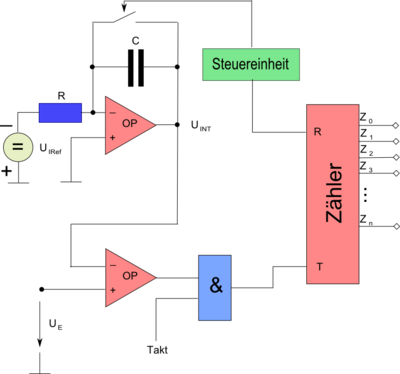
Zweiflanken-AD-Umsetzer (Dual-Slope)
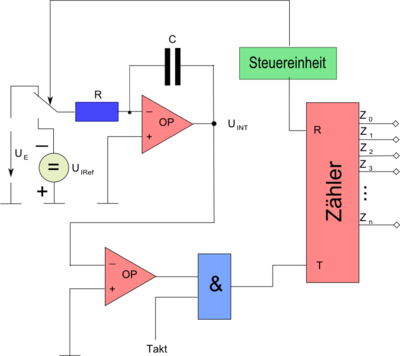
|
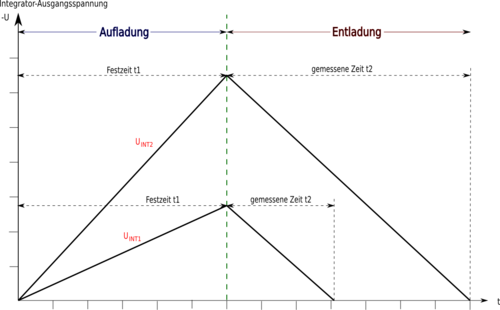
|
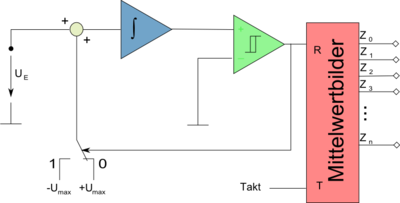
Sigma-Delta-Wandler
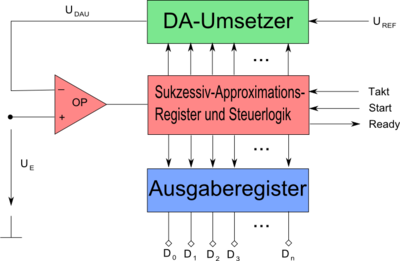
Wägeverfahren (sukzessive Approximation)
Diesem Verfahren kommt die größte technische Bedeutung zu, da es nur einen geringen Aufwand benötigt.