Formelsammlung Regelungstechnik
Formelsammlung für das Studienfach Regelungstechnik
Übertragungsglieder
| Bild | Name | Gleichung im Zeitbereich | Frequenzgangfunktion | Übertragungsfunktion |
|
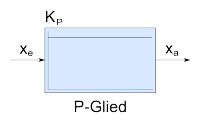
P-Glied | |||
|
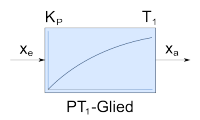
PT1-Glied | |||
|
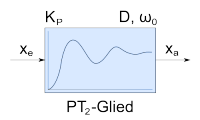
PT2-Glied | |||
|
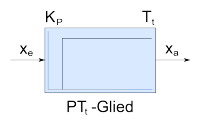
PTt-Glied | |||
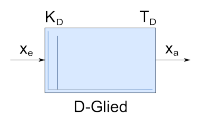
|
D-Glied |
|
|
|
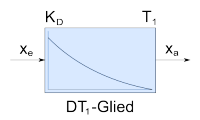
|
DT1-Glied | |||
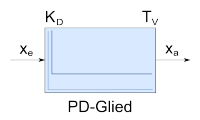
|
PD-Glied | |||
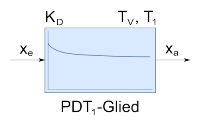
|
PDT1-Glied | ;
|
;
|
;
|
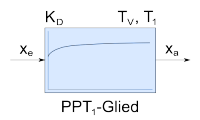
|
PPT1-Glied | ;
|
;
|
;
|
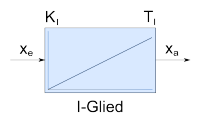
|
I-Glied |
|
|
|
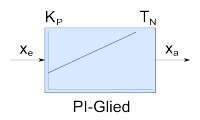
|
PI-Glied | |||
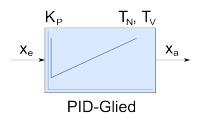
|
PID-Glied | |||
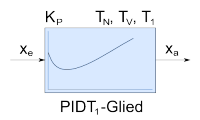
|
PIDT1-Glied |
|
Stabilität von Regelkreisen
Stabilitätskriterien
Hurwitz-Kriterium
Nyquist-Kriterium
|
Haben die Pole des offenen Kreises negative Realanteile und liegen höchstens zwei Pole bei , dann ist der geschlossene Kreis stabil, wenn die Ortskurve den kritischen Punkt (-1, j0) weder umschließt noch durchdringt, d.h., wenn der kritische Punkt links der Ortskurve liegt. |
Routh-Kriterium
Kompensationsreglerentwurf
PT1-Strecke
Der passende Regler nach dem Kompensationsverfahren ist der PI-Regler.
PT2-Strecke
Der passende Regler nach dem Kompensationsverfahren ist der PID-Regler.
IT1-Strecke
Der passende Regler nach dem Kompensationsverfahren ist der PD-Regler.
I-Strecke
Der passende Regler nach dem Kompensationsverfahren ist der P-Regler.