Formelsammlung Regelungstechnik: Unterschied zwischen den Versionen
MKastl (Diskussion | Beiträge) Die Seite wurde neu angelegt: „Formelsammlung für das Studienfach Regelungstechnik == Übertragungsglieder == {| width="100%" cellspacing="0" cellpadding="2" border="1" style="border-col…“ |
MKastl (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
{| width="100%" cellspacing="0" cellpadding="2" border="1" style="border-collapse: collapse;" | {| width="100%" cellspacing="0" cellpadding="2" border="1" style="border-collapse: collapse;" | ||
|- style="background: # | |- style="background: #558BC2;" | ||
| width="20%" align="left" | Bild | | width="20%" align="left" | Bild | ||
| width="20%" align="left" | Name | | width="20%" align="left" | Name | ||
| Zeile 139: | Zeile 139: | ||
<math>G_S(s) = \frac{K_P}{1 + T_S \cdot s}</math> | <math>G_S(s) = \frac{K_P}{1 + T_S \cdot s}</math> | ||
Der passende Regler nach dem Kompensationsverfahren ist der | Der passende Regler nach dem Kompensationsverfahren ist der PI-Regler. | ||
<math>G_R(s) = K_P \cdot \frac{1+T_NS}{T_N \cdot s}</math> | <math>G_R(s) = K_P \cdot \frac{1+T_NS}{T_N \cdot s}</math> | ||
| Zeile 147: | Zeile 147: | ||
<math>G_S(s) = \frac{K_P}{1 + 2D_ST_Ss+T^2_S s^2}</math> | <math>G_S(s) = \frac{K_P}{1 + 2D_ST_Ss+T^2_S s^2}</math> | ||
Der passende Regler nach dem Kompensationsverfahren ist der | Der passende Regler nach dem Kompensationsverfahren ist der PID-Regler. | ||
<math>G_R(s) = K_P \cdot \frac{1+T_Ns+T_NT_Vs^2}{T_N \cdot s}</math> | <math>G_R(s) = K_P \cdot \frac{1+T_Ns+T_NT_Vs^2}{T_N \cdot s}</math> | ||
| Zeile 155: | Zeile 155: | ||
<math>G_S(s) = \frac{1}{1 + T_Ss}\cdot\frac{K_I}{s}</math> | <math>G_S(s) = \frac{1}{1 + T_Ss}\cdot\frac{K_I}{s}</math> | ||
Der passende Regler nach dem Kompensationsverfahren ist der | Der passende Regler nach dem Kompensationsverfahren ist der PD-Regler. | ||
<math>G_S(s) = K_P( 1 + T_Vs )\,</math> | <math>G_S(s) = K_P( 1 + T_Vs )\,</math> | ||
| Zeile 163: | Zeile 163: | ||
<math>G_S(s) = \frac{K_I}{s}</math> | <math>G_S(s) = \frac{K_I}{s}</math> | ||
Der passende Regler nach dem Kompensationsverfahren ist der | Der passende Regler nach dem Kompensationsverfahren ist der P-Regler. | ||
<math>G_R(s) = K_P\,</math> | <math>G_R(s) = K_P\,</math> | ||
| Zeile 169: | Zeile 169: | ||
== Weblinks == | == Weblinks == | ||
[[Kategorie: | [[Kategorie:Regelungstechnik]] | ||
Aktuelle Version vom 7. Mai 2014, 06:49 Uhr
Formelsammlung für das Studienfach Regelungstechnik
Übertragungsglieder
| Bild | Name | Gleichung im Zeitbereich | Frequenzgangfunktion | Übertragungsfunktion |
|
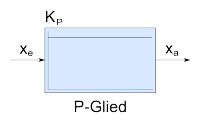
P-Glied | |||
|
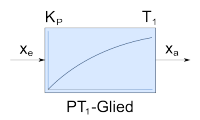
PT1-Glied | |||
|
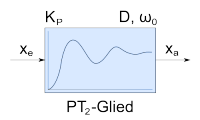
PT2-Glied | |||
|
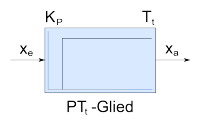
PTt-Glied | |||
|
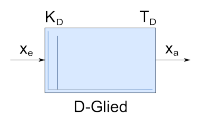
D-Glied |
|
|
|
|
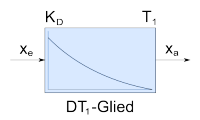
DT1-Glied | |||
|
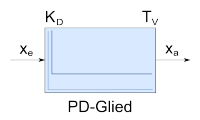
PD-Glied | |||
|
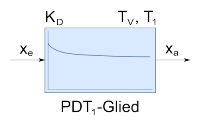
PDT1-Glied | ;
|
;
|
;
|
|
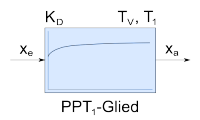
PPT1-Glied | ;
|
;
|
;
|
|
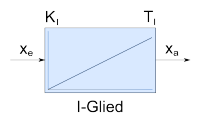
I-Glied |
|
|
|
|
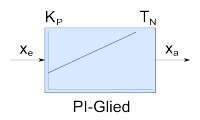
PI-Glied | |||
|
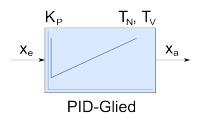
PID-Glied | |||
|
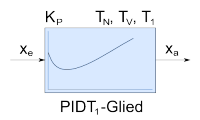
PIDT1-Glied |
|
Stabilität von Regelkreisen
Stabilitätskriterien
Hurwitz-Kriterium
Nyquist-Kriterium
|
Haben die Pole des offenen Kreises negative Realanteile und liegen höchstens zwei Pole bei , dann ist der geschlossene Kreis stabil, wenn die Ortskurve den kritischen Punkt (-1, j0) weder umschließt noch durchdringt, d.h., wenn der kritische Punkt links der Ortskurve liegt. |
Routh-Kriterium
Kompensationsreglerentwurf
PT1-Strecke
Der passende Regler nach dem Kompensationsverfahren ist der PI-Regler.
PT2-Strecke
Der passende Regler nach dem Kompensationsverfahren ist der PID-Regler.
IT1-Strecke
Der passende Regler nach dem Kompensationsverfahren ist der PD-Regler.
I-Strecke
Der passende Regler nach dem Kompensationsverfahren ist der P-Regler.